The Monty Hall trap by Phil Martin

"
Behind one of these three doors", shouts
Monty Hall, "
is the grand prize, worth one hundred thousand dollars! It's all yours if you pick the right door." "
I'll take door number one," you say. "
Let's see what's behind door number - No! Wait a minute!" says Monty Hall. "
Before we look, I'll offer you twenty thousand dollars, sight unseen, for whatever's behind door number one." "
No! No!" shouts the audience. "
Of course not," you say.
"
Even assuming the booby prizes are worth nothing, the expected value of my choice is thirty three and a third thousand dollars. Why should I take twenty thousand?" "
All right," says Monty Hall. "
But before we see what you've won, let's take a look behind door number two!" Door number two opens to reveal one of the booby prizes: a date in the National Open Pairs with Phil Martin. You and the audience breathe a sign of relief.
Simulatie "
I'll give you one last chance," says Monty Hall. "
You can have forty thousand dollars for what's behind door number one." "
No! No!" shouts the audience.
"
Sure," you say.
Simulatie 
If
Monty Hall had chosen a random door to open, you could calculate that you now had a 50-50 shot at the grand prize and would refuse the $40,000. But he didn't. Showman that he is, he intentionally showed you a booby prize to heighten the suspense.
Because you already knew that at least one of the other two doors held a booby prize, you have learned nothing. You still have the same one chance in three that you started with.
This scenario exemplifies a common probability trap:
treating biased information as random. Whenever the information itself has a direct bearing on whether or not you receive it, you must be careful to take that into account.
Here, the trap is easy to spot.* But the same trap can crop up more subtly in a bridge setting.
*Easy to spot? Ha!

About a year after this article was first published (Bridge Today Magazine, 1990), the Monty Hall problem appeared in Marilyn vos Savant's column in Parade magazine.
Ms. Savant , stated, as I had, that the probability of your having chosen the grand prize remained one third. She received more than 1,000 letters scoffing at this conclusion and demanding that she print a "
correction" and an apology. Many letters were from preeminent mathematicians and scientists.
Eventually, the debate found its way to the front page of the New York Times (July 21, 1991). In the end, the scoffers had to eat their words. But I forever lost my right to call this problem easy. - Phil Martin
Meer uitleg The Monty Hall trap in Bridge:
| Noord |
 A 5 A 5 |
 H 8 7 H 8 7 |
 B 5 3 B 5 3 |
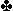 H B 7 4 2 H B 7 4 2 |
| Zuid |
 H 7 2 H 7 2 |
 A 6 4 2 A 6 4 2 |
 A 7 A 7 |
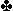 A 10 5 3 A 10 5 3 |
zuid 1 sans - noord 3 sans
Probleem 1: West start een kleine schoppen van een 5 kaart oost neemt en speelt schoppen terug, hoe speel je de klavers voor 5 slagen?
Probleem 2: West start een kleine schoppen van een 4 kaart oost neemt en speelt schoppen terug, hoe speel je de klavers voor 5 slagen?
Probleem 3: West start van een gebroken 4 kaart harten, hoe speel je de klavers voor 5 slagen?
Oplossing 1 : De redenering west heeft nog 8 vrije (13-5) plaatsen over en oost nog 10 gaat niet op. West is zijn langste kleur gestart en dat heeft consequenties. Stel aan de andere tafel zitten de tegenstanders ook in 3 sans, maar dan te spelen door de noordhand en oost start met ruiten zijn langste kleur. Moet je tegenstander anders snijden dan jij?
De relatieve distributie van de schoppenkleur is de lege deur uit het Monty Hall verhaal. Gemiddeld verwacht je 4,5 schoppens bij west en 3,5 bij oost. Het feitelijke zitsel 5-3 geeft west maar 1 kaart meer dan de verwachting. Nadat je klaver naar de heer gespeeld hebt, klaver opspeelt naar de aas en oost bekent, heeft west evenveel vrije plaatsen als oost. Speel west op klaver vrouw = 53%, slaan = 60%, speel oost op de vrouw = 60%.
Oplossing 2 : Spelen op slaan is niet goed a priori verwacht je 4,5 schoppens bij west. Nu hij schoppen is gestart is zijn maximum ruitenlengte 4 en zijn verwachte ruitenlengte ligt dus lager. Hoe korter west is in schoppen en ruiten, hoe meer klavers hij heeft. Speel west op klaver vrouw = 65%, slaan = 61%, speel oost op de vrouw = 48%.
Oplossing 3 : Na een hartenstart moet je west ook spelen op klavervrouw. Net als in oplossing 2 is de verwachte schoppen- en ruitenlengte afgenomen. Een vijfkaart kan niet en wegens de restricted choice zijn vierkaarten minder waarschijnlijk dus de klaverlengte neemt toe. Speel west op klaver vrouw = 67%, slaan = 60%, speel oost op de vrouw = 46%.
Bovenstaande geldt alleen als west zijn langste kleur start. Bij bepaalde biedingen zal hij dat niet doen, als bijvoorbeeld zijn langste kleur geboden is.
Als iemand 1 klaver opent en er 5 blijkt te hebben, is de kans dat hij een 5 kaart in een andere kleur heeft afgenomen.
Oftewel wat je zelf ontdekt beinvloedt de kansen en geeft je aanwijzingen omtrent de aanpak van een kleur. Wat de tegenstander je vertelt, door de uitkomst of door de bieding, geeft je nauwelijks informatie over hoe je een kleur aan moet spelen.
Notabene dit verhaal gaat niet meer op als de te starten kleur een zeskaart of langer is.
Uit het boek:
For experts only
Pamela and Matthew Granovetter
Meer uitleg Ik schud 52 kaarten jij pakt er 1, wat is de kans dat dit schoppenaas is?
1 op 52
Er zijn nu 2 stapels eentje van 1 kaart (jouw stapeltje) en eentje van 51 kaarten (mijn stapeltje)
Als je moest gokken in welk stapeltje zit schoppenaas?
Juist in mijn stapeltje 51/52.
Als ik 50 kaarten uit mijn stapeltje laat zien maakt dat wat uit?
Nee. (Je hebt niets geleerd je wist al dat er 51 kaarten niet schoppenaas waren)
Moet je switchen of bij je eerste keus (jouw stapeltje) blijven?
Natuurlijk moet je switchen, immers de kans dat schoppenaas bij mij zat was 51/52.

Monty Hall simulatie Monty Hall simulatie  "Behind one of these three doors", shouts Monty Hall, "is the grand prize, worth one hundred thousand dollars! It's all yours if you pick the right door."
"Behind one of these three doors", shouts Monty Hall, "is the grand prize, worth one hundred thousand dollars! It's all yours if you pick the right door." If Monty Hall had chosen a random door to open, you could calculate that you now had a 50-50 shot at the grand prize and would refuse the $40,000. But he didn't. Showman that he is, he intentionally showed you a booby prize to heighten the suspense.
If Monty Hall had chosen a random door to open, you could calculate that you now had a 50-50 shot at the grand prize and would refuse the $40,000. But he didn't. Showman that he is, he intentionally showed you a booby prize to heighten the suspense.  About a year after this article was first published (Bridge Today Magazine, 1990), the Monty Hall problem appeared in Marilyn vos Savant's column in Parade magazine.
About a year after this article was first published (Bridge Today Magazine, 1990), the Monty Hall problem appeared in Marilyn vos Savant's column in Parade magazine. 