The Monty Hall trap by Phil Martin

"
Behind one of these three doors", shouts
Monty Hall, "
is the grand prize, worth one hundred thousand dollars! It's all yours if you pick the right door." "
I'll take door number one," you say. "
Let's see what's behind door number - No! Wait a minute!" says Monty Hall. "
Before we look, I'll offer you twenty thousand dollars, sight unseen, for whatever's behind door number one." "
No! No!" shouts the audience. "
Of course not," you say.
"
Even assuming the booby prizes are worth nothing, the expected value of my choice is thirty three and a third thousand dollars. Why should I take twenty thousand?" "
All right," says Monty Hall. "
But before we see what you've won, let's take a look behind door number two!" Door number two opens to reveal one of the booby prizes: a date in the National Open Pairs with Phil Martin. You and the audience breathe a sign of relief.
"
I'll give you one last chance," says Monty Hall. "
You can have forty thousand dollars for what's behind door number one." "
No! No!" shouts the audience.
"
Sure," you say.

If
Monty Hall had chosen a random door to open, you could calculate that you now had a 50-50 shot at the grand prize and would refuse the $40,000. But he didn't. Showman that he is, he intentionally showed you a booby prize to heighten the suspense.
Because you already knew that at least one of the other two doors held a booby prize, you have learned nothing. You still have the same one chance in three that you started with.
This scenario exemplifies a common probability trap:
treating biased information as random. Whenever the information itself has a direct bearing on whether or not you receive it, you must be careful to take that into account.
Here, the trap is easy to spot.* But the same trap can crop up more subtly in a bridge setting.
*Easy to spot? Ha!

About a year after this article was first published (Bridge Today Magazine, 1990), the Monty Hall problem appeared in Marilyn vos Savant's column in Parade magazine.
Ms. Savant , stated, as I had, that the probability of your having chosen the grand prize remained one third. She received more than 1,000 letters scoffing at this conclusion and demanding that she print a "
correction" and an apology. Many letters were from preeminent mathematicians and scientists.
Eventually, the debate found its way to the front page of the New York Times (July 21, 1991). In the end, the scoffers had to eat their words. But I forever lost my right to call this problem easy. - Phil Martin
Meer uitleg The Monty Hall trap in Bridge:
| Noord |
 A 5 A 5 |
 H 8 7 H 8 7 |
 B 5 3 B 5 3 |
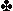 H B 7 4 2 H B 7 4 2 |
| Zuid |
 H 7 2 H 7 2 |
 A 6 4 2 A 6 4 2 |
 A 7 A 7 |
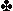 A 10 5 3 A 10 5 3 |
South one no trump - North three no trump
Problem 1: West leads a small spade from a five card, east wins and returns a spade. How to play the clubs for five tricks?
Problem 2: West leads a small spade from a four card, east wins and returns a spade. How to play the clubs for five tricks?
Probleem 3: West leads a small heart from a four card. How to play the clubs for five tricks?
Solution 1 : Reasoning west has 8 (13-5) vacant places and east has 10 is not correct. West leads his longest suit and that has consequences, say on the other table east has to lead, and he leads a diamond. Does that mean the leader at the other table has to play differently?
The relative distribution of the spade suit is the empty door from thet Monty Hall story. On average you expect 4.5 spades in west and 3.5 in east the 5-3 distribution gives west only 1 card more than the expectation After you play a club to the king you play a club to the ace if east follows suit, east has as many vacant places as west. Play west for the club queen=53%, play for the drop=60%, play east for the club queen=60.
Solution 2 : Playing for the drop is not correct west's maximum diamond length is four his expected diamond length is therefore lower. Shorter spades and diamonds means more clubs Play west for the club queen=65%, play for the drop=61%, play east for the club queen=48.
Solution 3 : After a heart lead you must play west for the club queen and like in solution 2 the expected diamond and spade length means more room for clubs Play west for the club queen=67%, play for the drop=60%, play east for the club queen=48.
From:
For experts only
Pamela and Matthew Granovetter
More explanation I shuffle a deck of 52 cards and you pick one.
What are the odds you pick the spade ace?
1 in 52.
There are now 2 decks of cards one containing 1 card (your deck) and one containing 51 cards (my deck).
If you have to guess in which deck is the spade ace you should say in my deck.
Does it matter if I show you 50 cards from my deck?
No you have learned nothing you already knew 51 cards are not the spade ace.
Do you have to switch decks?
Sure the odds the ace is in my deck are 51/52.

 "Behind one of these three doors", shouts Monty Hall, "is the grand prize, worth one hundred thousand dollars! It's all yours if you pick the right door."
"Behind one of these three doors", shouts Monty Hall, "is the grand prize, worth one hundred thousand dollars! It's all yours if you pick the right door." If Monty Hall had chosen a random door to open, you could calculate that you now had a 50-50 shot at the grand prize and would refuse the $40,000. But he didn't. Showman that he is, he intentionally showed you a booby prize to heighten the suspense.
If Monty Hall had chosen a random door to open, you could calculate that you now had a 50-50 shot at the grand prize and would refuse the $40,000. But he didn't. Showman that he is, he intentionally showed you a booby prize to heighten the suspense.  About a year after this article was first published (Bridge Today Magazine, 1990), the Monty Hall problem appeared in Marilyn vos Savant's column in Parade magazine.
About a year after this article was first published (Bridge Today Magazine, 1990), the Monty Hall problem appeared in Marilyn vos Savant's column in Parade magazine. 